Problem URL: https://leetcode.com/problems/range-sum-query-2d-immutable/

Dynamic programming solution for matrix range sum queries

Solution Approaches

Iterative Summation

Code

class NumMatrix:
    def __init__(self, matrix: list[list[int]]):
        self.matrix = matrix

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        n_sum = 0
        for i in range(row1, row2 + 1):
            n_sum += sum(self.matrix[i][col1:col2 + 1])
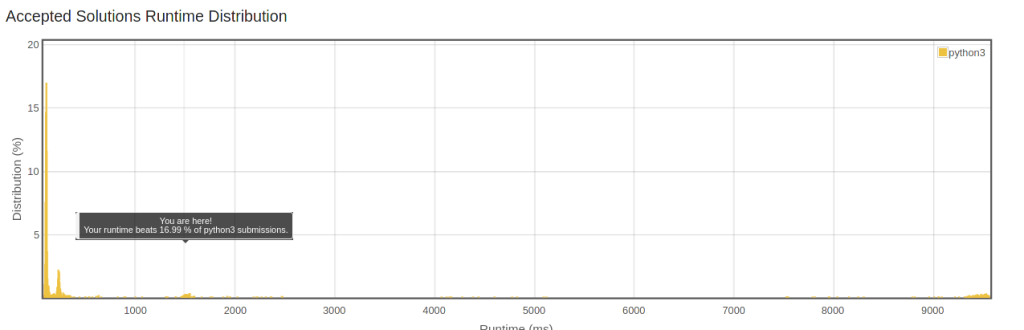
        return n_sum

LeetCode Test

Dynamic Programming

Code

class NumMatrix:
    def __init__(self, matrix: list[list[int]]):
        self.matrix = []
        last_row = None
        row_size = len(matrix[0])
        for row in matrix:
            row_sum = 0
            l_row = []
            if not last_row:
                for i in row:
                    row_sum += i
                    l_row.append(row_sum)
            else:
                l_row = []
                for i in range(row_size):
                    row_sum += row[i]
                    l_row.append(row_sum + last_row[i])
            self.matrix.append(l_row)
            last_row = l_row

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        row1_0 = row1 - 1
        col1_0 = col1 - 1
        if row1_0 >= 0 and col1_0 >= 0:
            n = self.matrix[row2][col2] - self.matrix[row2][
                col1_0] - self.matrix[row1_0][col2] + self.matrix[row1_0][
                col1_0]
        elif row1_0 < 0 and col1_0 >= 0:
            n = self.matrix[row2][col2] - self.matrix[row2][col1_0]
        elif row1_0 >= 0 and col1_0 < 0:
            n = self.matrix[row2][col2] - self.matrix[row1_0][col2]
        else:
            n = self.matrix[row2][col2]
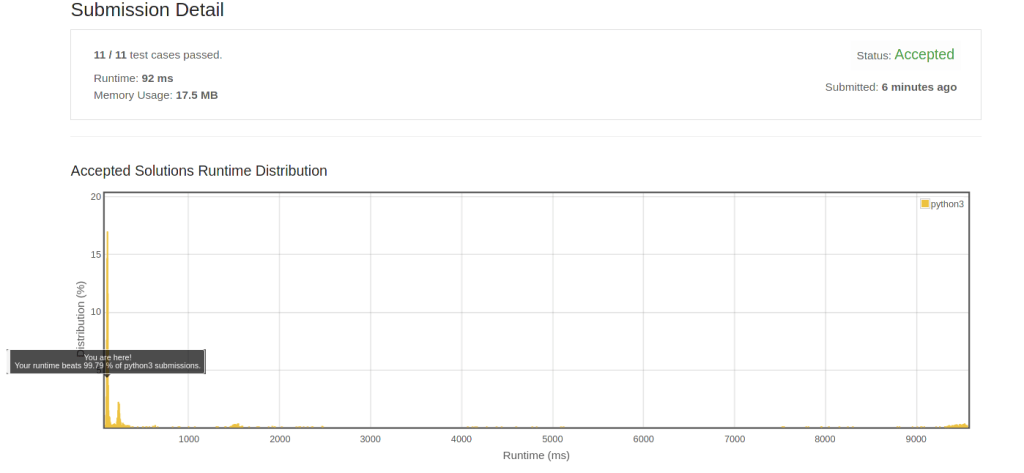
        return n

LeetCode Test

92ms / 17.5 MB (beats 99.79% / 20.87%).

Testing Method

a = NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]).sumRegion(2, 1, 4, 3)
print(a)

Summary

Dynamic programming essentially breaks down a large problem into smaller subproblems (almost stating the obvious).

The key optimization idea for this problem is to preprocess data during initialization specifically tailored for the target problem, thereby reducing time and space consumption during the final function call. That is, precompute matrix sums upfront rather than recalculating them during usage.

---